
Water Ripples with Vertex Shaders
WebGL, and therefore ThreeJS supports vertex shaders. And they are awesome. Why? Because they can do things on the GPU that would be costly or impossible on the CPU. Today we will make some water that looks like this:

This article is part of my ongoing series of medium difficulty ThreeJS tutorials. I’ve long wanted something in between the intro “How to draw a cube” and “Let’s fill the screen with shader madness” levels. So here it is.
To create water we need some geometry to start with. I’ve started with a plane 20 x 20 meters, divided in 10,000 sections (100x100).
new THREE.PlaneBufferGeometry(20,20,100,100)
I could use less segments but then the ripple effect would be more angular. If we are doing low poly this would be fine, but for today I want to really see the curves. Interestingly there is very little performance difference because once the geometry is uploaded to the GPU there is nothing for the CPU to do but update a time variable once per frame. Rad!
The plane is a mesh that looks like this:
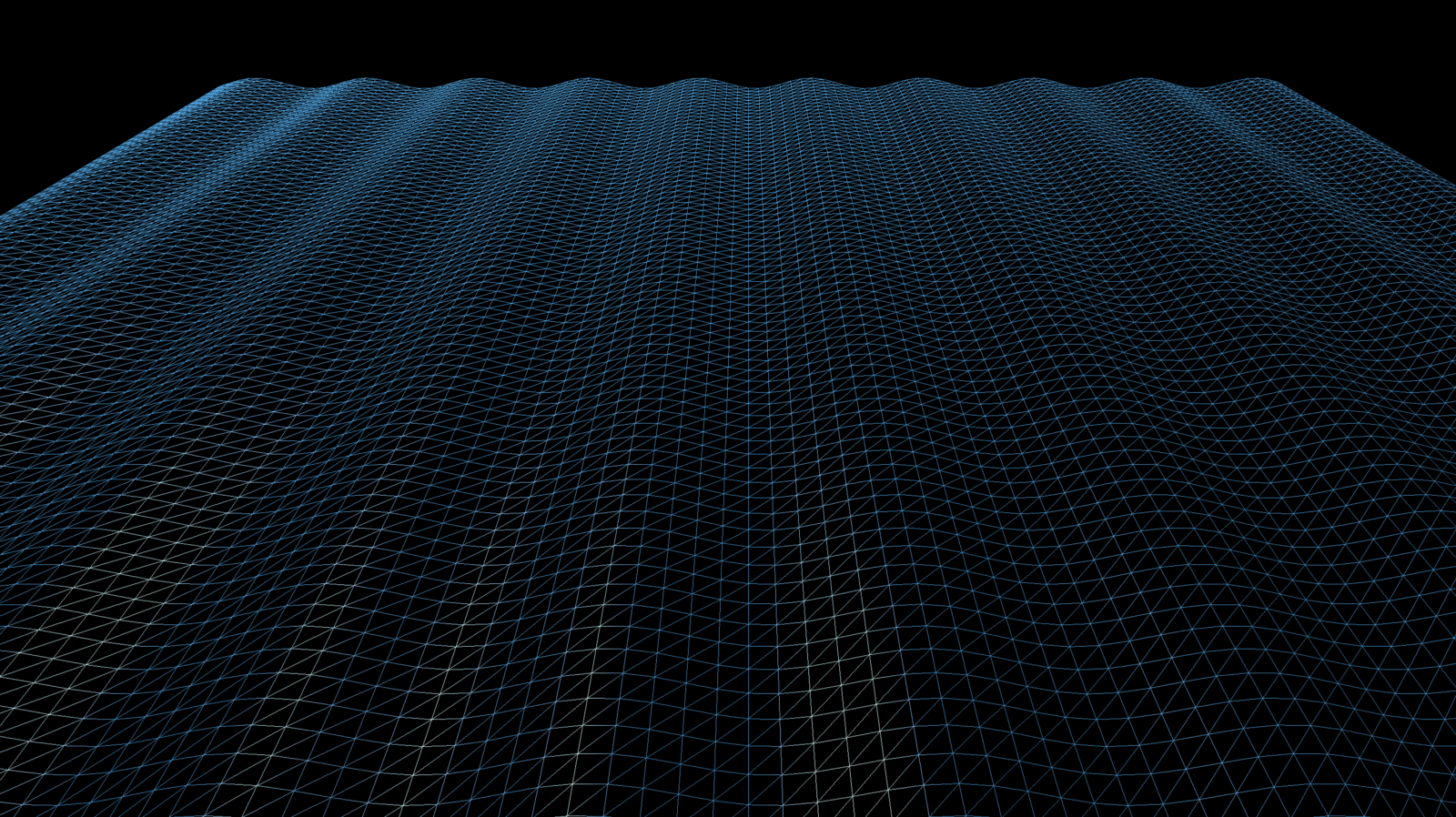
Like in the last blog, we will modify one of the standard ThreeJS materials to manipulate the vertex positions.
const mat = new THREE.MeshPhongMaterial({color:0x2288ff, shininess:100,})
mat.onBeforeCompile = (shader) => {
shader.uniforms.time = { value: 0}
shader.vertexShader = `
uniform float time;
` + shader.vertexShader
const token = '#include <begin_vertex>'
const customTransform = `
vec3 transformed = vec3(position);
float freq = 3.0;
float amp = 0.1;
float angle = (time + position.x)*freq;
transformed.z += sin(angle)*amp;
`
shader.vertexShader = shader.vertexShader.replace(token,customTransform)
matShader = shader
}
And in the render method we must update the time uniform:
render(time) {
if(matShader) matShader.uniforms.time.value = time/1000;
...
This moves the vertexes around using a sine wave based on the frequency and amplitude specified. If you look at the wire-frame you can see them moving in a nice sine wave. However, when the color is showing it doesn’t look very realistic.

There is no sense of waves in the middle, just at the edges. Why? Because we are changing the the positions of the points, but not the normals.
Fixing the normals
A normal is a vector pointing perpendicular to the surface of the mesh. There is a normal at every vertex, and since this mesh is a plane the normals are all pointing up.
The standard ThreeJS shaders use the normals to decide how light bounces off at that spot. Since we haven’t changed the normals it makes sense that the light, and therefore color, looks the same even though the positions have changed.
According to this StackOverflow question the formula for a calculating a surface normal is X(s,t) = ( s, t, A*sin((s+P)*F) ).
In code this would be :
objectNormal = normalize(vec3(-amp * freq * cos(angle),0.0,1.0));
vNormal = normalMatrix * objectNormal;
and now it looks right:

That’s it. Cool ripples. This technique can be easily extended too.
More examples
For example, suppose we need the ripples to go forward and back instead of left to right, just use the y coordinate instead of x.
vec3 transformed = vec3(position);
float freq = 3.0;
float amp = 0.1;
float angle = (time + position.y)*freq;
transformed.z += sin(angle)*amp;
objectNormal = normalize(vec3(0.0,-amp * freq * cos(angle),1.0));
vNormal = normalMatrix * objectNormal;

Or suppose we want a more complex wave equation that looks better, say adding a few sine waves together:
uniform float time;
float wave(float time, float freq, float amp) {
float angle = (time+position.y)*freq;
return sin(angle)*amp;
}
float waveNorm(float time, float freq, float amp) {
float angle = (time+position.y)*freq;
return -amp * freq * cos(angle);
}
...
vec3 transformed = vec3(position);
float freq = 3.0;
float amp = 0.1;
transformed.z += wave(time,freq,amp)
+ wave(time,freq*2.0,amp/2.0)
+ wave(time,freq*3.5,amp*0.2)
;
float normWave = waveNorm(time,freq,amp)
+ waveNorm(time,freq*2.0,amp/2.0)
+ waveNorm(time,freq*3.5,amp*0.2)
;
objectNormal = normalize(vec3(0.0, normWave,1.0));
vNormal = normalMatrix * objectNormal;

Or make ripples expand out from the center instead of the edge
vec3 transformed = vec3(position);
float dx = position.x;
float dy = position.y;
float freq = sqrt(dx*dx + dy*dy);
float amp = 0.1;
float angle = -time*10.0+freq*6.0;
transformed.z += sin(angle)*amp;
objectNormal = normalize(vec3(0.0,-amp * freq * cos(angle),1.0));
vNormal = normalMatrix * objectNormal;

Displacing vertexes with equations is a very powerful way to create cool effects in ThreeJS at almost zero CPU cost.
Next time we’ll explore some other ways to customize geometry.
Get Noticed
By the way, if you are working on a cool WebVR experience that you’d like to have showcased right inside Firefox Reality, let us know.